今日推荐文章
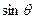
若+,∈(0,π),则tan=.答案:

下列角的终边位于第二象限的是()A.B.C.D.答案:B

已知f(x)是定义在R上的偶函数,且在区间(﹣∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(﹣),则a的取值范围是()A.(﹣∞,﹣)∪(﹣,+∞)B.(﹣∞,﹣)C.(﹣,+∞)D.(﹣,﹣)答案:A【解答】解:∵函数f(x)是偶函数,∴f(3|2a+1|)>f(﹣),等价为f(3|2a+1|)>f(),∵偶函数f(x)在区间(﹣∞,0)上单调递减,∴f(x)在区间[0,+∞)上单调递增,∴3|2a+1|>,即2a+1<﹣或2a+1>,解得a<﹣或a>﹣,
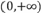
已知定义在区间上的函数满足:,,恒有,且当时,.(1)证明:函数在区间上为单调递减函数.(2)若,解不等式.答案:1)设,则,因为,所以,即,所以,所以在区间上为单调递减函数.(2)因为,所以,而,所以.因为,即,由得,即,所以.故不等式的解集为.
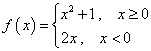
设函数,若,则_________.答案:3
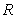
已知定义在上的函数满足,当时,。(1)求,判断的奇偶性并证明。(2)若,解不等式。答案:(1)令,令为奇函数。(2),令,则,所以为定义域上的减函数,解得
在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AA1=BC=5.M是BC中点,则直线A1M与平面ABC所成角的正切值为()A.B.2C.D.3答案:B【解析】根据平面,即可找到为直线与平面所成角,计算即可.【详解】因为平面,所以为直线与平面所成角.在中,,,.故选【点睛】本题主要考查直线与平面所成角的求法,根据直线垂直平面找到直线与平面所成角为解题的关键,属于简单题.
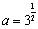
若,,,则()A.B.C.D.答案:B

集合A={x∈N|1≤x<4}的真子集的个数是()A.16B.8C.7D.4答案:C
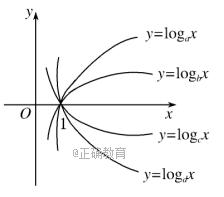
函数y=logax,y=logbx,y=logcx,y=logdx的图象如下图所示,则a,b,c,d的大小顺序是()A、1<d<c<a<bB、c<d<1<a<bC、c<d<1<b<aD、d<c<1<a<b答案:C
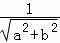
若直线l:ax+by=1与圆C:x2+y2=1有两个不同交点,则点P(a,b)与圆C的位置关系是()A.点在圆上B.点在圆内C.点在圆外D.不能确定答案:C解:直线l:ax+by=1与圆C:x2+y2=1有两个不同交点,则<1,∴a2+b2>1,点P(a,b)在圆C外部,
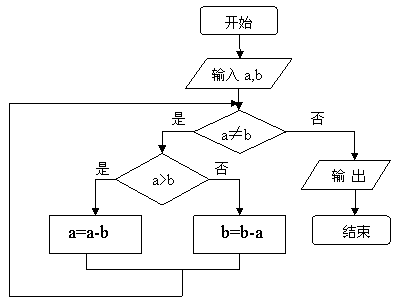
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4D.14答案:B
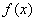
函数是定义在上的函数,且对任意的正实数均有:,则不等式的解集是()A.B.C.D.答案:D
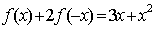
已知,则是()A.B.C.D.答案:A
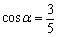
若,且α在第四象限,则tanα=()A.B.C.D.答案:D
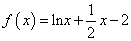
使得函数有零点的一个区间是()A.B.C.D.答案:.C【解析】由题意可得函数的定义域,∵,,,由函数零点的判定定理可知,函数在上有一个零点,故选C.
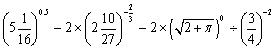
计算:;答案:原式,.…………………………5分
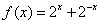
已知函数.(Ⅰ)试写出这个函数的性质(不少于3条,不必说明理由),并作出图像;(Ⅱ)设函数,求这个函数的最小值.答案:解析:(1)偶函数;定义域;值域;单调递增区间:,单调递减区间:等-----4分图像略.-----6分(2)设,则,设时,‚时所以,时,‚时�
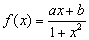
已知函数是定义在(-1,1)上的奇函数,且(1)求的解析式;(2)证明:函数在(-1,1)上是增函数;解关于t的不等式.答案:(I),;(Ⅱ)任取所以函数在上是增函数(Ⅲ)
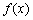
函数在单调递增,且为奇函数,若,则满足的的取值范围是().A.B.C.D.答案:D是奇函数,故;又是增函数,,即则有,解得,