-
-
Word文档版
学考宝(xuekaobao.com)友情提示:html格式不完整,如有需要请根据文末提示下载并进行二次校对Word文档。
9.4 矩形、菱形和正方形训练题
一、选择题
1.下列命题为假命题的是( )
A.对角线相等的平行四边形是矩形
B.对角线互相垂直的平行四边形是菱形
C.有一个内角是直角的平行四边形是正方形
D.有一组邻边相等的矩形是正方形
2.平行四边形ABCD的对角线AC和BD交于点O,添加一个条件不能使平行四边形ABCD变为矩形的是( )
A.OD=OC B.∠DAB=90° C.∠ODA=∠OAD D.AC⊥BD
3.下列给出的条件中,不能判定一个四边形是矩形的是( )
A.一组对边平行且相等,一个角是直角
B.对角线互相平分且相等
C.有三个角是直角
D.一组对边平行,另一组对边相等,且对角线相等
4.如图,边长为的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是( )
A. B. C. D.
5.如图,菱形的对角线与相交于点O,E为边的中点,连结.若,则( )
A.2 B.2.5 C.3 D.4
6.如图,长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在点处,点D落在点处,若,则( )
A. B. C. D.
第4题图 第5题图 第6题图
7.如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
8.如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
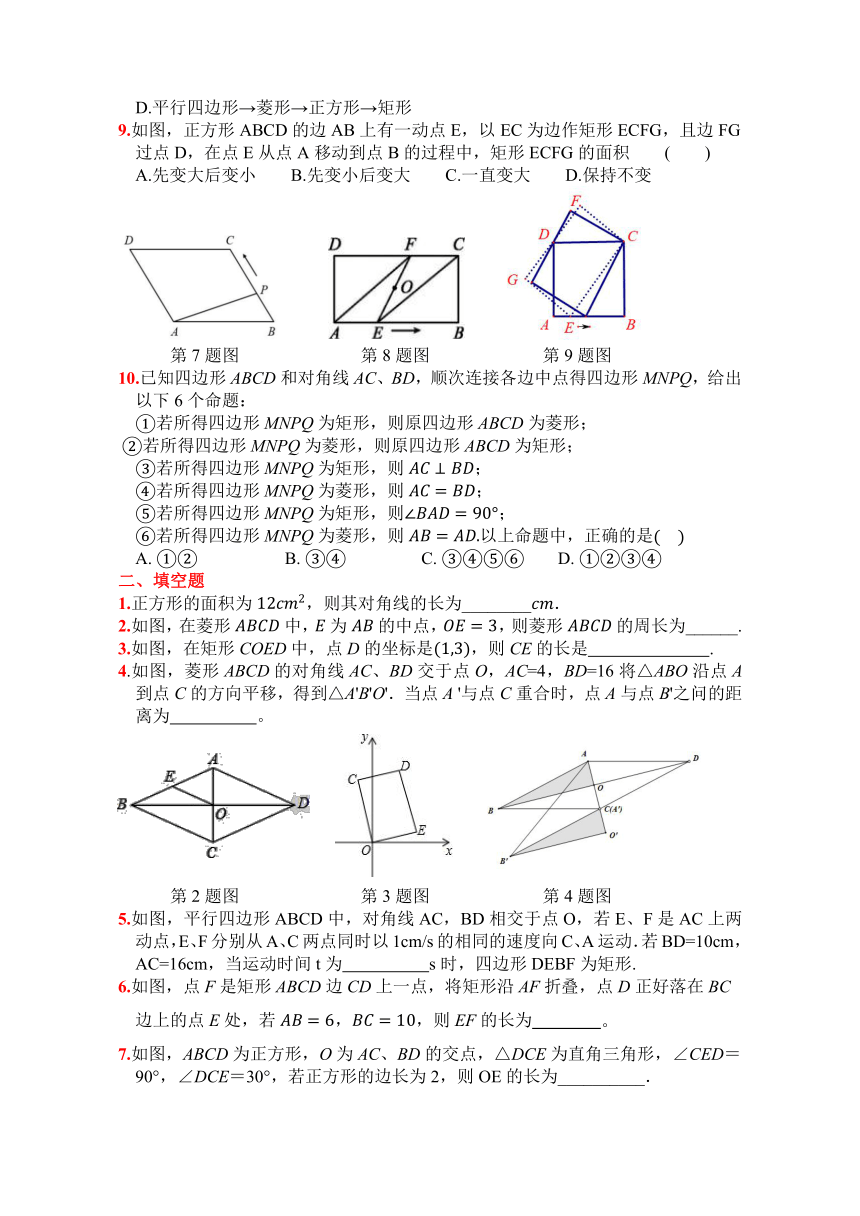
9.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积 ( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
第7题图 第8题图 第9题图
10.已知四边形ABCD和对角线AC、BD,顺次连接各边中点得四边形MNPQ,给出以下6个命题:
若所得四边形MNPQ为矩形,则原四边形ABCD为菱形;
若所得四边形MNPQ为菱形,则原四边形ABCD为矩形;
若所得四边形MNPQ为矩形,则;
若所得四边形MNPQ为菱形,则;
若所得四边形MNPQ为矩形,则;
若所得四边形MNPQ为菱形,则以上命题中,正确的是
A. B. C. D.
二、填空题
1.正方形的面积为,则其对角线的长为________.
2.如图,在菱形中,为的中点,,则菱形的周长为______.
3.如图,在矩形COED中,点D的坐标是,则CE的长是 .
4.如图,菱形ABCD的对角线AC、BD交于点O,AC=4,BD=16将△ABO沿点A到点C的方向平移,得到△A'B'O'.当点A '与点C重合时,点A与点B'之问的距离为 。
第2题图 第3题图 第4题图
5.如图,平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动.若BD=10cm,AC=16cm,当运动时间t为 s时,四边形DEBF为矩形.
6.如图,点F是矩形ABCD边CD上一点,将矩形沿AF折叠,点D正好落在BC边上的点E处,若,,则EF的长为
7.如图,ABCD为正方形,O为AC、BD的交点,△DCE为直角三角形,∠CED=90°,∠DCE=30°,若正方形的边长为2,则OE的长为__________.
第5题图 第6题图 第7题图
8.如图,菱形ABCD的边长为4,,E为BC的中点,在对角线AC上存在一点P,使的周长最小,则的周长的最小值为 。
9.如图,正方形ABCD的边长为a,对角线AC和BD相交于点O,正方形的边交AB于点E,OC1交BC于点F,正方形绕O点转动的过程中,与正方形ABCD重叠部分的面积为______(用含a的代数式表示)
10.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中,,,对角线与交于点O,点E为边上的一个动点,,,垂足分别为点F,G,则___________.
第8题图 第9题图 第10题图
三、解答题
1.(2023·四川乐山)如图,在中,,点D为边上任意一点(不与点A、B重合),过点D作,,分别交、于点E、F,连接.
(1)求证:四边形是矩形;
(2)若,求点C到的距离.
2.(2022·四川南充)如图,在菱形中,点E,F分别在边上,,分别与交于点M,N.求证:(1).(2).
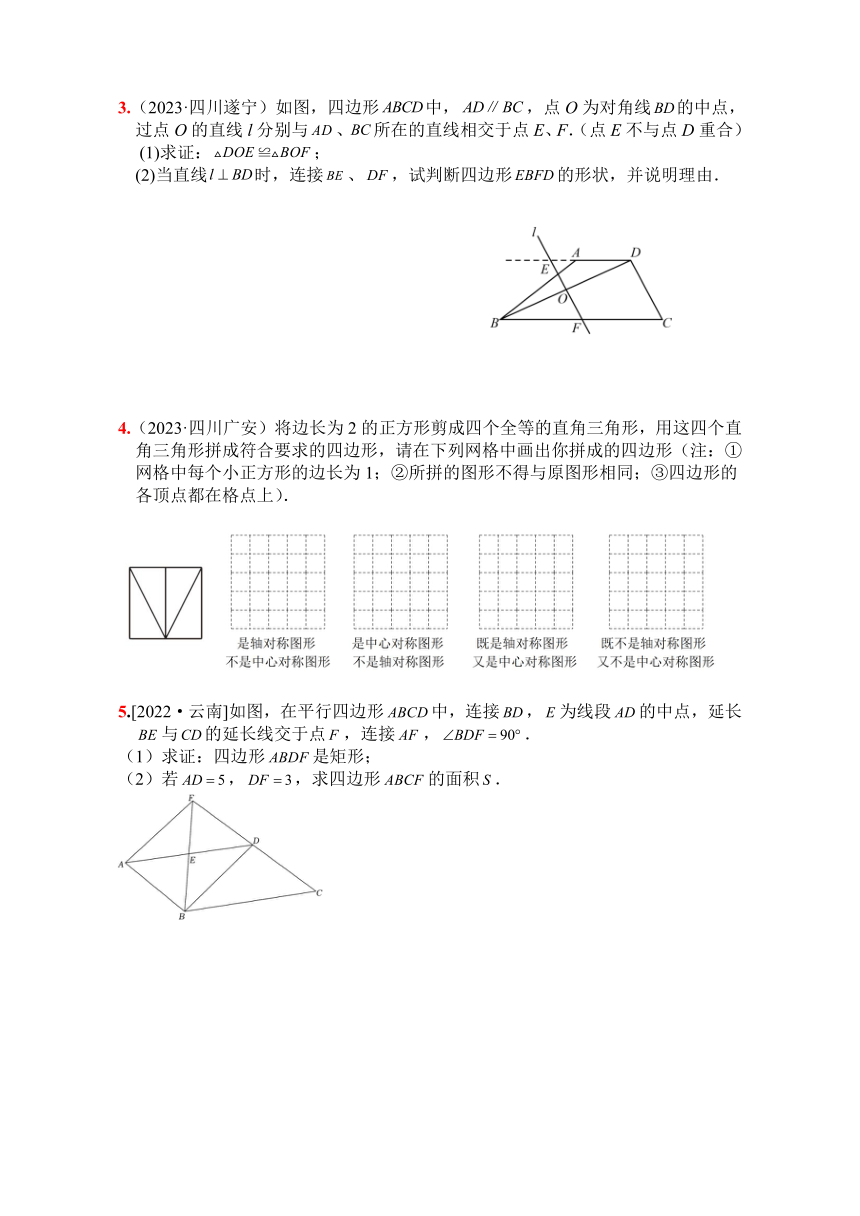
3.(2023·四川遂宁)如图,四边形中,,点O为对角线的中点,过点O的直线l分别与、所在的直线相交于点E、F.(点E不与点D重合)
(1)求证:;
(2)当直线时,连接、,试判断四边形的形状,并说明理由.
4.(2023·四川广安)将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
5.[2022·云南]如图,在平行四边形中,连接,为线段的中点,延长与的延长线交于点,连接,.
(1)求证:四边形是矩形;
(2)若,,求四边形的面积.
6.如图1,在正方形ABCD中,点E是边AB上的一个动点点E与点A,B不重合,连接CE,过点B作于点G,交AD于点F.
求证:≌;
如图2,连接EF、CF,若,求四边形BEFC的面积;
如图3,当点E运动到AB中点时,连接DG,求证:.
参考答案
一、选择题
1.C;2.D;3.D;4.C;5.B;6.C;7.C;8.B;9.D;10.B;
二、填空题
1.;2.24;3.;4.10 ;5.3或13;6.;7.;8.;9.;10.
三、解答题
1.【解析】(1)证明:∵,,
∴四边形为平行四边形,
∵,∴四边形是矩形.
(2)解:∵,,
∴
设点C到的距离为h,
∵
∴∴答:点C到的距离为.
2.(1)证明:由菱形的性质可知,,,
∵ ,∴,即,
在和中,,∴.
(2)证明:如图,连接BD交AC于点O,
由菱形的性质可知,,∴,
由(1)知,∴,,
∴,∴,
在和中,,∴.∴,
∴,∴.
3.(1)证明:∵点O为对角线的中点,∴,
∵,∴,,
在和中,
,∴;
(2)解:四边形为菱形,理由如下:
连接、,如图所示:
根据解析(1)可知,,∴,
∵,∴四边形为平行四边形,
∵,即,∴四边形为菱形.
4.解:①要求是轴对称图形但不是中心对称图形,则可作等腰梯形,如图四边形ABCD即为所求;
②要求是中心对称图形但不是轴对称图形,则可作一般平行四边形,如图四边形ABCD即为所求;
③要求既是轴对称图形又是中心对称图形,则可作菱形、矩形等,如图四边形ABCD即为所求;
④要求既不是轴对称图形又不是中心对称图形,则考虑作任意四边形,如图四边形ABCD即为所求.
5.解:(1)证明:四边形是平行四边形,,.
点是的中点,.
在和中,,,.
又,四边形是平行四边形.
.四边形是矩形.
(2)由(1)得四边形是矩形,,,.
.
,.
四边形是平行四边形,.
.四边形的面积.
6.证明:,,
,
四边形ABCD是正方形,,,
,,
在和中,
,≌;
解:≌,,
四边形BEFC的面积的面积的面积
;
证明:如图3,过点D作于H,
设,
点E是AB的中点,
,
,
在中,,
,
,
,,
,
,,
≌,
,
,
,,
;
图片资源预览